Convection Is A Mode Of Heat Transfer For Which Types Of Objects?

The Second Law

The second law of thermodynamics states that rut transfer occurs spontaneously only from higher to lower temperature bodies.

Learning Objectives

Contrast the concept of irreversibility between the Commencement and 2nd Laws of Thermodynamics

Central Takeaways

Primal Points

• Many thermodynamic phenomena, allowed to occur by the first constabulary of thermodynamics, never occur in nature.
• Many processes occur spontaneously in one direction only, and the 2d police of thermodynamics deals with the direction taken by spontaneous processes.
• According to the second law of thermodynamics, it is impossible for whatever process to have oestrus transfer from a cooler to a hotter object as its sole result.

Primal Terms

• entropy: A measure of how evenly energy (or some analogous belongings) is distributed in a organization.
• the commencement law of thermodynamics: A version of the police of conservation of energy, specialized for thermodynamical systems. Usually expressed every bit ΔU=Q−W.

Irreversibility

The second law of thermodynamics deals with the direction taken by spontaneous processes. Many processes occur spontaneously in one direction only—that is, they areirreversible, under a given set of conditions. Although irreversibility is seen in twenty-four hours-to-day life—a broken glass does non resume its original state, for example—complete irreversibility is a statistical statement that cannot exist seen during the lifetime of the universe. More precisely, an irreversible process is one that depends on path. If the process can go in merely i direction, then the reverse path differs fundamentally and the process cannot exist reversible.

For example, heat involves the transfer of energy from higher to lower temperature. A cold object in contact with a hot one never gets colder, transferring heat to the hot object and making it hotter. Furthermore, mechanical free energy, such as kinetic energy, can be completely converted to thermal energy by friction, simply the opposite is impossible. A hot stationary object never spontaneously cools off and starts moving. Yet another example is the expansion of a puff of gas introduced into one corner of a vacuum chamber. The gas expands to fill the sleeping room, but information technology never regroups in the corner. The random movement of the gas molecules could have them all back to the corner, but this is never observed to happen.

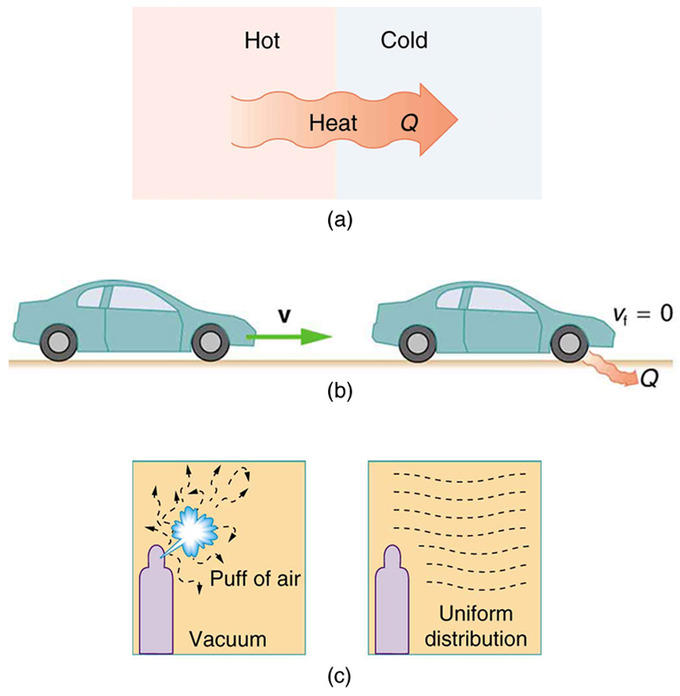
One-Manner Candy in Nature: Examples of one-way processes in nature. (a) Heat transfer occurs spontaneously from hot to cold and not from cold to hot. (b) The brakes of this motorcar convert its kinetic energy to heat transfer to the environment. The contrary procedure is impossible. (c) The outburst of gas allow into this vacuum sleeping accommodation quickly expands to uniformly fill every part of the chamber. The random motions of the gas molecules will never render them to the corner.

2nd Law of Thermodynamics

The fact that certain processes never occur suggests that there is a police forbidding them to occur. The start law of thermodynamics would allow them to occur—none of those processes violate conservation of energy. The police force that forbids these processes is called the second law of thermodynamics. Nosotros shall come across that the 2nd law tin be stated in many ways that may seem different, only these many ways are, in fact, equivalent. Like all natural laws, the 2d police force of thermodynamics gives insights into nature, and its several statements imply that it is broadly applicable, fundamentally affecting many apparently disparate processes. The already familiar direction of oestrus transfer from hot to cold is the basis of our first version of the 2d law of thermodynamics.

Thermodynamics and Estrus Engines: A brief introduction to heat engines and thermodynamic concepts such every bit the Carnot Engine for students.

The Second Constabulary of Thermodynamics(first expression): Rut transfer occurs spontaneously from higher- to lower-temperature bodies simply never spontaneously in the reverse direction.

The law states that it is impossible for whatever procedure to take as its sole outcome estrus transfer from a libation to a hotter object. We will express the police force in other terms later on, most importantly in terms of entropy.

Heat Engines

In thermodynamics, a oestrus engine is a system that performs the conversion of heat or thermal energy to mechanical work.

Learning Objectives

Justify why efficiency is ane of the most important parameters for any heat engine

Key Takeaways

Key Points

• A cyclical procedure brings a system, such every bit the gas in a cylinder, back to its original land at the terminate of every cycle. Nearly oestrus engines, such as reciprocating piston engines and rotating turbines, use cyclical processes.
• The second law of thermodynamics can be expressed as the following: It is incommunicable in any system for heat transfer from a reservoir to completely convert to work in a cyclical process in which the system returns to its initial state.
• The efficiency of a heat engine (Eff) is defined to exist the engine's cyberspace work output Westward divided past estrus transfer to the engine: [latex]\text{Eff} = \frac{\text{Westward}}{\text{Q}_\text{h}} = 1 - \frac{\text{Q}_\text{c}}{\text{Q}_\text{h}}[/latex], where Q_c and Q_h denotes heat transfer to hot (engine) and cold (surroundings) reservoir.

Primal Terms

• thermal energy: The internal energy of a system in thermodynamic equilibrium due to its temperature.
• internal energy: The sum of all energy nowadays in the system, including kinetic and potential energy; equivalently, the energy needed to create a system, excluding the energy necessary to readapt its surroundings.

In thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work. Gasoline and diesel engines, jet engines, and steam turbines are all oestrus engines that do work by using part of the rut transfer from some source. Estrus transfer from the hot object (or hot reservoir) is denoted as Q_h, while heat transfer into the cold object (or common cold reservoir) is Q_c, and the work washed past the engine is W. The temperatures of the hot and cold reservoirs are T_h and T_c, respectively.

Heat Transfer: (a) Estrus transfer occurs spontaneously from a hot object to a cold one, consistent with the 2nd law of thermodynamics. (b) A rut engine, represented here by a circle, uses part of the rut transfer to do piece of work. The hot and cold objects are called the hot and cold reservoirs. Qh is the estrus transfer out of the hot reservoir, W is the work output, and Qc is the rut transfer into the cold reservoir.

Thermodynamics and Estrus Engines: A brief introduction to heat engines and thermodynamic concepts such as the Carnot Engine for students.

Because the hot reservoir is heated externally, which is energy intensive, information technology is important that the work is done as efficiently as possible. In fact, we would similar W to equal Q_h, and for there to exist no heat transfer to the surroundings (Q_c=0). Unfortunately, this is impossible. The second police force of thermodynamics (second expression) too states, with regard to using heat transfer to do work: Information technology is impossible in any system for heat transfer from a reservoir to completely convert to work in a cyclical process in which the system returns to its initial state.

A cyclical process brings a organization, such equally the gas in a cylinder, back to its original state at the end of every bike. Most oestrus engines, such every bit reciprocating piston engines and rotating turbines, apply cyclical processes. The second constabulary, in its 2nd form, clearly states that such engines cannot have perfect conversion of heat transfer into work done.

Efficiency

A cyclical procedure brings the system back to its original condition at the end of every wheel. Past definition, such a system's internal energy U is the same at the beginning and end of every cycle—that is, ΔU=0. The start law of thermodynamics states that ΔU=Q−West, where Q is the net heat transfer during the wheel (Q=Q_h−Q_c) and W is the net work done by the arrangement. Since ΔU=0 for a complete wheel, we have W=Q. Thus the net piece of work done by the system equals the cyberspace oestrus transfer into the arrangement, or

[latex]\text{W} = \text{Q}_\text{h} - \text{Q}_\text{c}[/latex] (cyclical process),

just as shown schematically in (b).

Efficiency is one of the most important parameters for whatever heat engine. The problem is that in all processes, there is meaning heat transfer Q_c lost to the environment. In the conversion of free energy to work, nosotros are e'er faced with the trouble of getting less out than we put in. Nosotros define the efficiency of a heat engine (Eff) to be its net piece of work output Due west divided by oestrus transfer to the engine Q_h:

[latex]\text{Eff} = \frac{\text{Due west}}{\text{Q}_\text{h}}[/latex].

Since West=Q_h−Q_c in a cyclical procedure, we can also express this as

[latex]\text{Eff} = \frac{\text{Q}_\text{h} - \text{Q}_\text{c}}{\text{Q}_\text{h}} = 1 - \frac{\text{Q}_\text{c}}{\text{Q}_\text{h}}[/latex] (for cyclical process),

making it clear that an efficiency of i, or 100%, is possible only if in that location is no heat transfer to the environment (Q_c=0).

Carnot Cycles

The Carnot cycle is the most efficient cyclical procedure possible and uses just reversible processes through its bicycle.

Learning Objectives

Analyze why the Carnot engine is considered the perfect engine

Key Takeaways

Key Points

• The 2nd police force of thermodynamics indicates that a Carnot engine operating betwixt two given temperatures has the greatest possible efficiency of any oestrus engine operating betwixt these ii temperatures.
• Irreversible processes involve dissipative factors, which reduces the efficiency of the engine. Obviously, reversible processes are superior from the efficiency perspective.
• Carnot efficiency, the maximum doable rut engine efficiency, is given as [latex]\text{Eff}_\text{c} = ane-\frac{\text{T}_\text{c}}{\text{T}_\text{h}}[/latex].

Key Terms

• the second law of thermodynamics: A law stating that states that the entropy of an isolated organization never decreases, because isolated systems spontaneously evolve toward thermodynamic equilibrium—the state of maximum entropy. Equivalently, perpetual motion machines of the 2d kind are impossible.
• heat engine: Any device which converts oestrus energy into mechanical work.

Nosotros know from the second law of thermodynamics that a estrus engine cannot exist 100 pct efficient, since there must always exist some rut transfer Q_c to the environment. (See our cantlet on "Heat Engines. ") How efficient can a oestrus engine be and then? This question was answered at a theoretical level in 1824 by a young French engineer, Sadi Carnot (1796-1832), in his written report of the so-emerging heat engine technology crucial to the Industrial Revolution. He devised a theoretical cycle, now chosen the Carnot cycle, which is the most efficient cyclical process possible. The second police of thermodynamics can exist restated in terms of the Carnot cycle, and then what Carnot really discovered was this cardinal law. Any rut engine employing the Carnot cycle is called a Carnot engine.

What is crucial to the Carnot wheel is that merely reversible processes are used. Irreversible processes involve dissipative factors, such as friction and turbulence. This increases heat transfer Q_c to the environment and reduces the efficiency of the engine. Obviously, then, reversible processes are superior.

The second law of thermodynamics (a third form): A Carnot engine operating between two given temperatures has the greatest possible efficiency of any heat engine operating between these two temperatures. Furthermore, all engines employing only reversible processes have this same maximum efficiency when operating between the same given temperatures.

Efficiency

The Carnot cycle comprises two isothermal and ii adiabatic processes. Recall that both isothermal and adiabatic processes are, in principle, reversible.

PV Diagram for a Carnot Cycle: PV diagram for a Carnot bicycle, employing but reversible isothermal and adiabatic processes. Heat transfer Qh occurs into the working substance during the isothermal path AB, which takes place at constant temperature Th. Oestrus transfer Qc occurs out of the working substance during the isothermal path CD, which takes place at constant temperature Tc. The net piece of work output West equals the area inside the path ABCDA. Also shown is a schematic of a Carnot engine operating between hot and cold reservoirs at temperatures Th and Tc.

Carnot likewise determined the efficiency of a perfect rut engine—that is, a Carnot engine. It is always true that the efficiency of a cyclical oestrus engine is given by: [latex]\text{Eff} = \frac{\text{Q}_\text{h} - \text{Q}_\text{c}}{\text{Q}_\text{h}} = 1-\frac{\text{Q}_\text{c}}{\text{Q}_\text{h}}[/latex].

What Carnot found was that for a perfect rut engine, the ratio Q_c/Q_h equals the ratio of the absolute temperatures of the rut reservoirs. That is, Q_c/Q_h=T_c/T_h for a Carnot engine, and so that the maximum or Carnot efficiency Eff_C is given past [latex]\text{Eff}_\text{c} = one-\frac{\text{T}_\text{c}}{\text{T}_\text{h}}[/latex], where T_h and T_c are in kelvins. (Derivation of the formula is slightly across the scope of this atom. ) No existent estrus engine can do every bit well as the Carnot efficiency—an actual efficiency of about 0.7 of this maximum is unremarkably the best that can be accomplished.

Heat Pumps and Refrigerators

A heat pump is a device that transfers heat free energy from a heat source to a heat sink against a temperature slope.

Learning Objectives

Explain how the the components of a heat pump cause rut to transfer from a common cold reservoir to a hot reservoir

Key Takeaways

Central Points

• A oestrus pump 's mission is for heat transfer Qh to occur into a warm environment, such equally a abode in the winter.
• The mission of air conditioners and refrigerators is for heat transfer Qc to occur from a cool surround, such every bit chilling a room or keeping nutrient at lower temperatures than the environs.
• A heat pump can be used both to oestrus and absurd a space. It is essentially an air conditioner and a heating unit all in ane. This is fabricated possible past reversing the flow of its refrigerant, changing the direction net rut transfer.

Fundamental Terms

• CFC: An organic compound that was commonly used as a refrigerant. Non normally used anymore because of its ozone depletion effect.

Heat pumps, air conditioners, and refrigerators utilize oestrus transfer from cold to hot. Estrus transfer (Q_c) occurs from a cold reservoir and into a hot one. This requires piece of work input W, which is as well converted to oestrus transfer. Thus the estrus transfer to the hot reservoir is Q_h=Q_c+W. A heat pump'southward mission is for oestrus transfer Q_h to occur into a warm environment, such as a dwelling house in the wintertime. The mission of air conditioners and refrigerators is for heat transfer Q_c to occur from a cool environment, such as chilling a room or keeping food at lower temperatures than the environment. Really, a heat pump can be used both to rut and cool a infinite. It is essentially an air conditioner and a heating unit all in i. In this section we will concentrate on its heating mode.

Oestrus Pumps

A working fluid such equally a non-Cfc refrigerant is used in a basic rut pump. The basic components of a heat pump in are a condenser, an expansion valve, an evaporator and a compressor. In the outdoor coils (the evaporator), heat transfer Q_c occurs to the working fluid from the common cold outdoor air, turning it into a gas. The electrically driven compressor (work input Due west) raises the temperature and pressure of the gas and forces information technology into the condenser coils that are inside the heated space. Because the temperature of the gas is higher than the temperature inside the room, oestrus transfer to the room occurs and the gas condenses to a liquid. The liquid then flows back through a pressure level-reducing valve to the outdoor evaporator coils, being cooled through expansion. (In a cooling cycle, the evaporator and condenser coils exchange roles and the period direction of the fluid is reversed. )

Simple Heat Pump: A unproblematic rut pump has four basic components: (1) condenser, (two) expansion valve, (3) evaporator, and (4) compressor.

Coefficient of Performance

The quality of a heat pump is judged by how much heat transfer Q_h occurs into the warm space compared with how much work input W is required. Nosotros ascertain a heat pump's coefficient of performance (COP_hp) to exist

[latex]\text{COP}_{\text{hp}} = \frac{\text{Q}_\text{h}}{\text{W}}[/latex].

Since the efficiency of a estrus engine is Eff=W/Q_h, we see that COP_hp=i/Eff. Since the efficiency of any heat engine is less than 1, information technology means that COP_hp is always greater than one—that is, a heat pump always has more oestrus transfer Q_h than work put into information technology. Another interesting point is that rut pumps piece of work best when temperature differences are small. The efficiency of a perfect engine (or Carnot engine) is

[latex]\text{Eff}_\text{C}=i\frac{\text{T}_\text{c}}{\text{T}_\text{h}}[/latex];

thus, the smaller the temperature difference, the smaller the efficiency and the greater the COP_hp.

Air Conditioners and Refrigerators

Air conditioners and refrigerators are designed to cool something down in a warm surround. As with oestrus pumps, work input is required for heat transfer from cold to hot. The quality of air conditioners and refrigerators is judged by how much heat transfer Q_c occurs from a cold environment compared with how much work input West is required. What is considered the do good in a heat pump is considered waste heat in a fridge. We thus define the coefficient of operation (COP_ref) of an air conditioner or refrigerator to exist

[latex]\text{COP}_{\text{ref}} = \frac{\text{Q}_\text{c}}{\text{Due west}}[/latex].

Since Q_h=Q_c+Due west and COP_hp=Q_h/West, nosotros derive that

[latex]\text{COP}_{\text{ref}} = \text{COP}_{\text{hp}} -i[/latex].

Likewise, from Q_h>Q_c, we meet that an air conditioner will have a lower coefficient of performance than a heat pump.

Source: https://courses.lumenlearning.com/boundless-physics/chapter/the-second-law-of-thermodynamics/

Posted by: knightwhave1995.blogspot.com

Share this post